Photo by Camille Brodard on Unsplash
This blog post is a part of “Blockchain for Test Engineers” series.
In previous articles, we have already discussed hash functions and their usage. Today I propose to learn about an exciting data structure built using hashes - Merkle Tree.
Blockchain and transactions
A blockchain is a chain of data blocks connected cryptographically (each subsequent block points to the previous one).
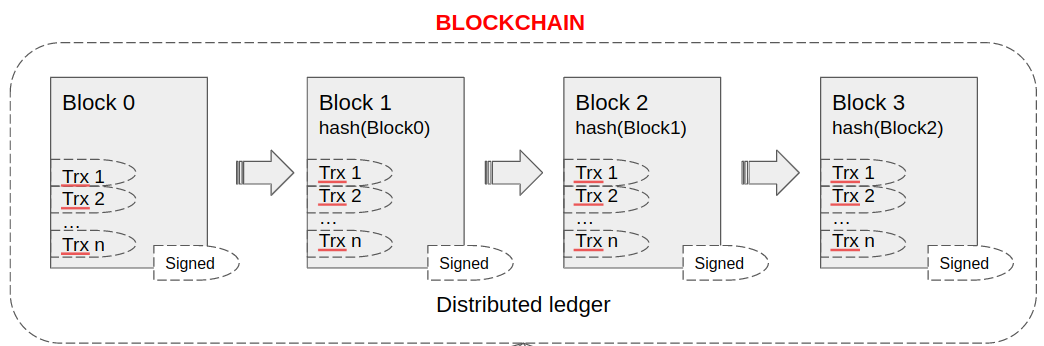
In addition, each block stores a lot of other interesting information: the hash of the block itself, the number of transactions, the complexity of the mining algorithm, and more. But most importantly - each block contains a set of validated transactions.
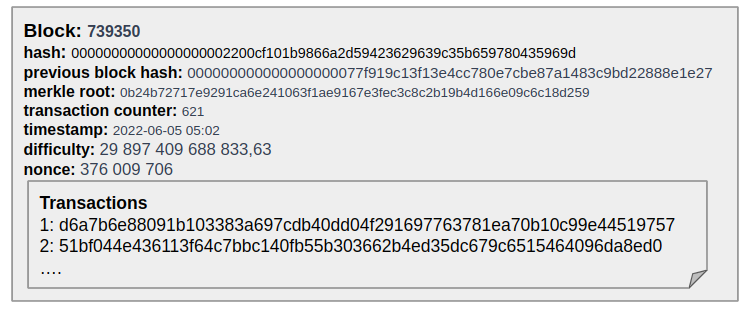
But how can a user verify that a transaction is inside the block? Wasn’t it changed during the mining phase?
In the simplest case, the user must download the entire blockchain to his computer and check the required blocks. Each block takes up, on average, about 1MB. Therefore, the transaction verification process can take a long time (and requires hard disk space too).
But there is a way to check transactions quickly and with a much smaller data set than the whole block? The answer is yes - it is Merkle tree data structure.
What is Merkle Tree?
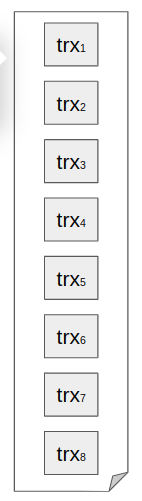
Imagine that we have eight transactions ready to be included in the block:
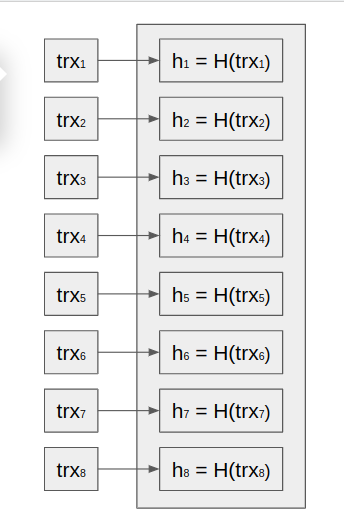
Apply hash functions to each transaction:
Let’s concatentate each pair of hashes and then hash the result:
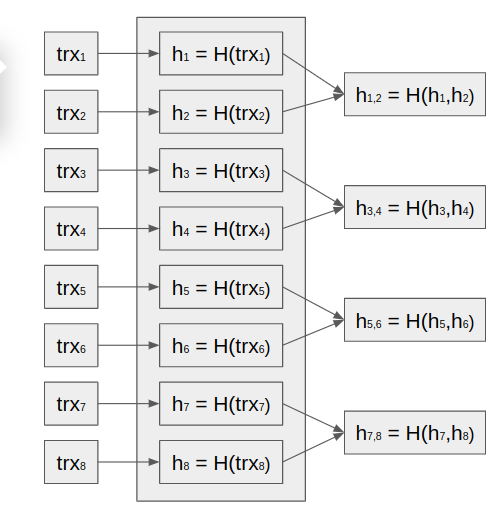
We will continue the pairing and hashing processes until we get a single value:
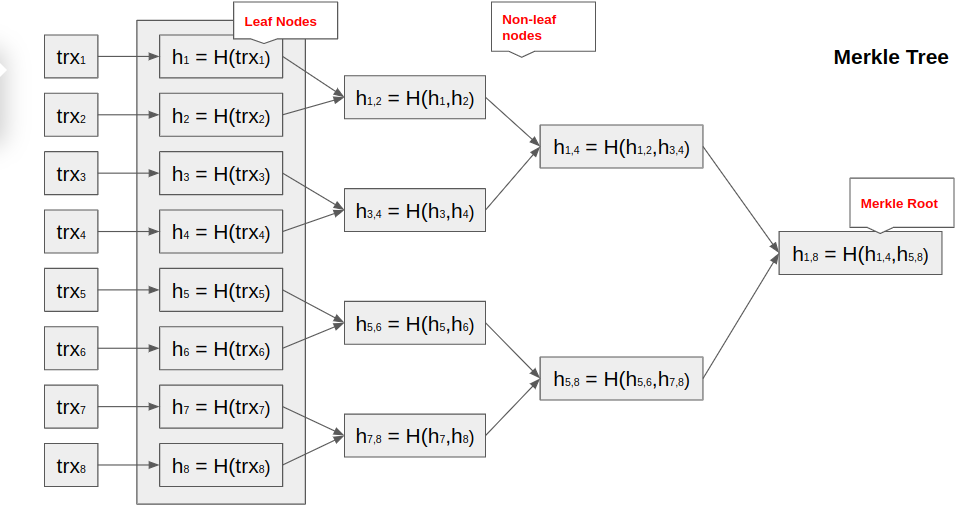
The resulting binary tree is called a Merkel Tree. The last hash obtained is the tree’s root (Merkle Root). This root is also a part of the header of each block in the Bitcoin blockchain.
Other parts of the Merkle Tree are non-leaf nodes and leaf nodes.
What is the meaning of the Merkle Tree?
The advantage of organizing transactions in the form of Merkle Tree manifests when we check the integrity of the transaction.
In a simple case you can download all eight transactions, then generate a leaf nodes and recreate the process of creating a tree from scratch. And then - compare the resulting root of the tree with the one stored inside the block.
We can do it for a dozen transactions. But if there are thousands of transactions? Or millions, or maybe more? For example, some projects can contain billions of Merkle Tree leaves. So to re-create the tree, you need to compute a vast amount of hashes with the O(n) complexity.
Merkle Proofs allows you to mathematically check the integrity of the transaction without the need to download and recreate all transactions. You need to perform much fewer operations.
For example, we need to check transaction 2. In this case, we need to have Merkle Tree root and Merkle Proof for this transaction:
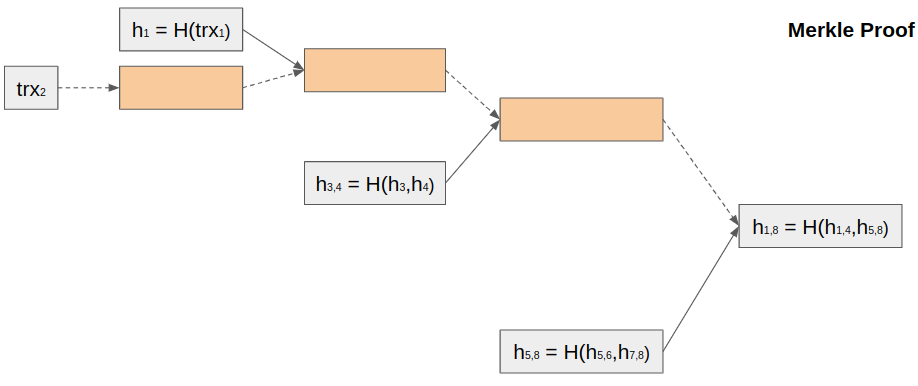
In our example, the proof contains only 3 hashes and another 4 hashes we need to calculate to get a Merke Root. Otherwise, we will need to download 8 transactions and calculate 15 hashes.
Instead of donwloading n transactions, we need to download O(log n)-sized Merkle Proof and also - Merkle Root.
In the Bitcoin blockchain, if we need to verify that transaction is indeed in the block, we need to download the block header (80 bytes instead of 1MB block) and then request Merkle Proof for a specific transaction. As a result, we can unambiguously check the integrity of the transaction with much lower resource costs.
Merkle Tree is used in Bitcoin’s “light” clients (Simple Payment Verification nodes) to quickly validate if transaction belongs to a particular block.
Where you can find Merkle Trees?
It turns out, that Merkle Trees are used in many modern systems:
